2014-NIPS-[Ramp]Analysis of Learning from Positive and Unlabeled Data

これも東大杉山研じゃないか、たまげたな。

前にやったPU Learningは、強い分布に対しての仮定が必要だった。つまり、PositiveなDataのうちから一様に抽出して、ラベル付きになっているという強い分布への仮定が必要だった。今回のやつはそこへのカウンターも兼ねた理論的な証明。

問題設定

Positive(+1)とNegative(-1)の誤分類を最小化する関数は以下のように書ける。これは、誤分類の割合を表す関数。

まず、あるデータ $X$ について、ラベル付けする識別器 $f(X) \in 1, -1$ があるとする。また、

$R_{-1}(f) = P_{-1} (f(X) \neq -1)$ 　本来Negative=-1なのに、識別器にPositive=1に分類されてしまう確率。
$R_{1}(f) = P_{1} (f(X) \neq 1)$ 　本来Positive=1なのに、識別器にNegative=-1に分類されてしまう確率
$\pi$ は全sampleのうちのpositiveの割合であり、 $\frac{n_{pos}}{n_{pos} + n_{neg}}$ で推定する。

R(f) = \pi R_1(f) + (1-\pi) R_{-1}(f)

なお、01損失を使っている以上、この損失 $R(f)$ は誤り率そのものである。

また、ここから更にcost-sensitive=重み付き分類は、上記の式にcostのc_1, c_{-1}をつけたもの。これは以下のもの。結局後述するCost-SensitiveなPUの式は、このようなPN分類の重み付きに帰着できるよ。

R(f) = \pi c_1 R_1(f) + (1-\pi) c_{-1} R_{-1}(f)

上の式はPositive=1とNegative=-1だったが、PU分類ではUnknownにNegativeが全部入ってるし、Positiveも一部ある。 $\pi$ は前述のとおり、全sampleでのPositiveな割合。(Positiveなラベルしかつけないというけどさすがにsampleを見る限りNegativeが何個あったかも把握はしておくので、 $\pi$ が求まる。これがラベルなしのデータでも同じ割合であると推定)この時、↓の式のように、ラベル付けされてないものの確率を求めることができる。

P_X = \pi P_1 + (1-\pi) P_{-1}

次に、 $R_X(f)$ =分類器f(X)が、P_Xに対してその中でPositiveの確率として、求めてみる。つまり $\pi$ では？と思うが、 $\pi$ は全体のPositiveな真の割合であり、 $R_X(f)$ は推定してるといえる。
これ、ある訓練データから一部をPositiveとしてラベル付けしておくかたちだが、多分ラベルなしは、訓練データでのNegativeを除く。排除しないと、割合が $\pi$ で推定できないから(Negativeが予想以上に混入するので)。

R_X (f) = P_X (f(X) = 1) = \pi P_1(f(X) = 1) + (1 - \pi) P_{-1} (f(X) = 1) \\ = \pi(1 - R_1(f)) + (1 - \pi) R_{-1}(f)

となる。ここで、 $P_1(f(X)=1) = 1 - P_1(f(X)=-1)$ を使った。これは、Positiveデータにおいて、Positiveであると正解する確率は、余事象として1からPositiveデータにおいてNegativeデータであると正解する確率を引いたものに等しいから(二値分類なので)

後続研究ではこの代入を使わずに、そのまま $R_1(f)$ に直さずに解いて、 $l(z)-l(-z)$ に着目した。この論文では後述するように、この代入をすることで、 $l(z) + l(-z)$ に着目している。

📄2015-ICML-[uPU] Convex Formulation for Learning from Positive and Unlabeled Data

この $R_X$ 、ラベルなしのクラス $P_X$ のうち、識別器にpositiveと認識される確率であるだが、これを使って $R(f)$ も表してみる。なんせPU分類には $R_{-1}$ は分からないから、できるだけ消したい。重みは一旦なしで見る。

R(f) = \pi R_1(f) + (1-\pi) R_{-1}(f) \\ = \pi R_1(f) + R_X(f) - \pi(1 - R_1(f)) \\ = 2\pi R_1(f) + R_X(f) - \pi

そして、 $\mu$ を $P_X$ に対して $P_1$ が占める割合とする。今までは $\pi$ で、Negativeも入れた中でのSampleのPositiveの割合だった。

しかし、 $\mu$ は、ラベル付き=Positiveとラベルなし(Negativeの割合は使わない！)ということ。

この $\mu$ という量を使って、 $R(f)$ を無理やり式変形してみる。

R(f) = \frac{2 \pi}{\mu} \cdot \mu R_1(f) + \frac{1}{1 - \mu} \cdot (1 - \mu) R_X(f) - \pi

このように、はじめにいった重み付きのPN分類に帰着できるとわかるね。

実用的な話は上の $2 \pi R_1(f) + R_X(f) - \pi$ を最小化するで終わっていて、これは帰着できるというだけの話である。その帰着の過程で、Unlabeledの損失 $R_X$ はNegative例の扱いである。

損失関数について

ここで定める損失関数は正解=正であるほど小さい値をとって、不正解ほど大きな値をとる。

ヒンジ損失関数を考える。=ReLU関数。

L_H(z) = \frac{1}{2}\max (0, 1 - z)

ランプ損失関数を考える。

L_R(z) = \frac{1}{2} \max (0, \min(2, 1 - z))

PN分類における損失の違い

PN分類では、Ramp損失のほうが使われず、Hinge損失を基本的に使う。

理由としては、

分離可能性。損失の和が0なら、すべてのサンプルにおいて損失が0。これは両方の損失で成り立つ。
- サンプルが分離可能である場合、Ramp損失で0になるならHinge損失でも0になる。なので、最適化しやすいHinge損失のほうがやっぱりいい。
Hinge損失は凸関数である。凸関数の合成となると最適化しやすい。
- Hinge損失は-1を下回っても傾きは-1であるが、Ramp損失は-1を下回ると傾きは0になって、+1以上特別がつかなくなり学習に一部支障が出るようになる。
- なお、この一部の区間以外の傾きを0にするのはカットオフである。

PU分類ではRamp損失のほうがいい

Ramp損失は左右対称なので、以下の式が成り立つ。

L_R(z) + L_R(-z) = 1

PU分類の損失の式を分解すると以下のようになる。

2 \pi R_1(f) + R_X(f) - \pi \\ = 2 \pi \mathbb{E} _{+1}[l(g(X))] + \{ \pi \mathbb{E}_{+1}[l(-g(X))] + (1 - \pi) \mathbb{E}_{-1}[l(g(X))] \} \\ = \{ \pi \mathbb{E}_{+1}[l(g(X)) + l(-g(X))]\} + \pi \mathbb{E}_{+1} [l(g(X))] + (1 - \pi) \mathbb{E}_{-1} [l(-g(X))]

ここで、Ramp損失なら前の項が定数なので、実際の最適化で考慮しなくていい。Hinge損失なら考慮することになり、最適化の項が増えて結果的に難しくなる。

つまり、凸だから最適化しやすい以上に、項が増えることによって実際の最適化が難しくなってしまうということ。

実演

中心-3, 分散1をPositive、中心+3, 分散1をNegativeとする。この一次元データを線形分類器で、異なるclass priorで分類すると考える。これは大体かぶってない。

この時、以下のようになってしまう。

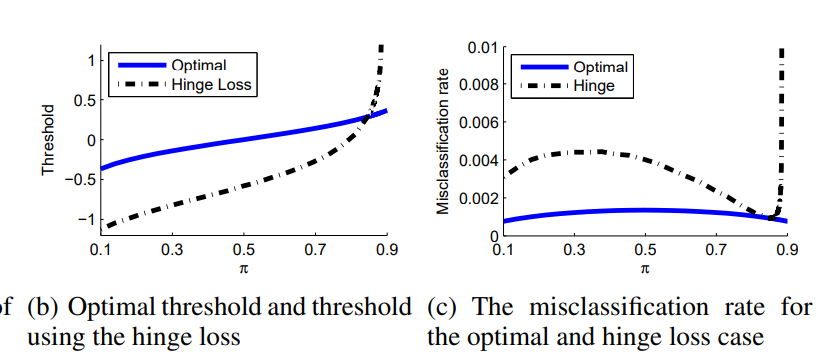
Ramp損失はOptimalの青い線と全く同じになるらしい。

このようにHinge損失で実際に最適化するとなかなかうまくいかないとわかる。

つまり、実際の最適はでは $2 \pi R_1(f) + R_X(f)$ の最小化をするが、結果的にキャンセルできるRamp損失を使うと計算するうえで性能が良くなるということ。

Class Priorの推定

$\pi = Pr[y=+1]$ を推定することが重要。間違った推定がどれほどの影響をもたらすかを考察する。

01損失については、 $\pi R_1(f) + (1 - \pi)R_{-1}(f)$ という式になる。この時 $\pi$ が0か1の時損失は必ず0になる。それ以外では分離可能ではない限り、ふっくらとした以下のような凸関数になる。

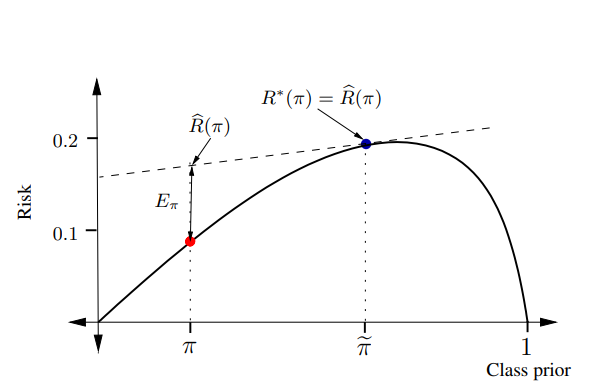
この中で、我々が限られたデータから学習できるのは $\hat{R}(\pi)$ であり、これが実線の $R^*(\pi)$ と等しいのが望ましい。

これがPUになると、推測された $\hat{\pi}$ から以下の式の最小化になる。

R(f) = 2 \hat{\pi} R_1(f) + R_X(f) - \hat{\pi}

ここで、推測した $\hat{\pi}$ は $R_X$ の内部の組成に関係はないため、 $R_X(f) = \pi(1 - R_1(f)) + (1 - \pi)R_{-1}(f)$ のままである。これを意識して式変形すると以下のようになる。

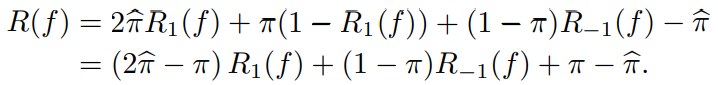
$R_1$ の係数が正である必要があるので、悪くとも $\hat{\pi} \leq \pi/2$ である必要がある(高く推測しすぎてはだめ)

さらに、以下のように $\tilde{\pi}$ を定義する。これは上の $R_1, R_{-1}$ の係数を正規化したもの。

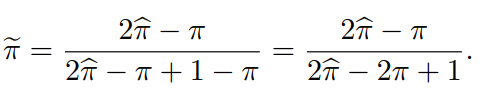
結果としては以下の式になる。

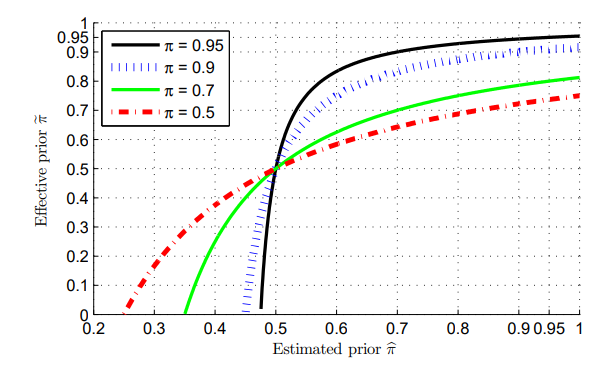
$\pi$ が十分に大きければ、推測するClass Prior $\hat{\pi}$ が大きく変わっても、損失関数の最小化をするときにかかっている係数 $\tilde{\pi}$ から見れば大して変わらないということ。

PU分類の誤差 in 同一分布じゃない

注意：他の論文を読んでたら、ここでは前提として「Positiveでラベル付けされてるものとされてないものは同じ分布に従う」とあるらしい。じゃあこれはなんだ...?

PU分類は、同一分布に従う必要がある。つまり、ラベル付けでPositiveになってるのは、Positive全体のデータからランダムに抽出させないとアカン。
では、同一分布に従ってない時(=ランダムに抽出してない？)はどうする？その時の誤差はどうなるのか、を解析したのがこの論文。

関数 $f(\mathbf{x})$ を次のように定める。

f(\mathbf{x}) = \sum _{i = 1}^{n} \alpha_i k(\mathbf{x}_i, \mathbf{x}) + \sum _{j = 1}^{n ^\prime} \alpha_j ^\prime k(\mathbf{x}_j^\prime, \mathbf{x})

$\alpha_1, \cdots, \alpha_n, \alpha_1^\prime, \cdots, \alpha_{n^\prime}^\prime$ は実数。
$\mathbf{x}_1, \cdots, \mathbf{x}_nは、p(\mathbf{x} | y = +1)$ 。Positiveの分布に従い、ランダムに\mathbf{x}_iをn個抽出した。
$\mathbf{x}_1^\prime, \cdots, \mathbf{x} _{n^{ \prime }} ^ \primeは、p(\mathbf{x})$ 。つまり、これはPositive、Negative関係なくランダムに $\mathbf{x}_i^\prime$ を $n^\prime$ 個抽出した。

つまり、n個のPositiveと、 $n^\prime$ 個のラベルなしがあるとして、それらと引数 $\mathbf{x}$ のカーネル内積の一定係数の線形結合。この関数での誤差を考えてみる。

これをごにょごにょすると(中略...)

一定分布に従わないという最悪な状況でも、誤差は

O(\frac{1}{\sqrt{n}} + \frac{1}{\sqrt{n^\prime}})

のオーダーになる。これは $n$ 個が独立同分布に従って得られ、 $n^\prime$ 個がまた別の独立同分布に従ってる場合に最適である。

もし、いずれも同じ独立同分布に従ってるなら、

O(\frac{1}{\sqrt{n + n^\prime}})

だが、これは非現実的。同じ独立同分布に従ってるなら、PU Learningする意味ないので。

ただ、これを見る限り、どれほど分布が違っていようが、完全に一致の分布から $n$ と $n^\prime$ を取ってるのと比べて、たかだか $2 \sqrt{2}$ 倍までしか悪くならない！